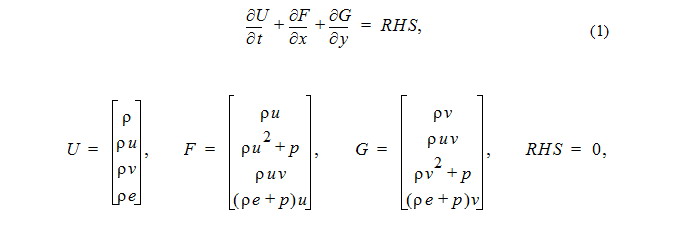
3-2. Basic Equations
Equations of motion (2D flow)
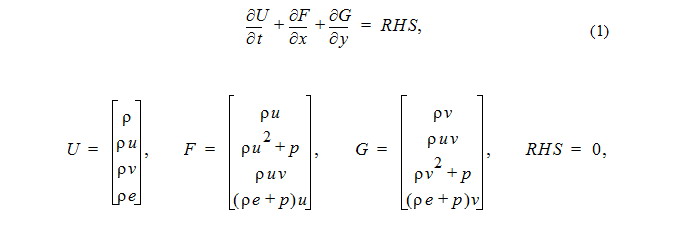
RHS = 0, d/dt = 0: Steady inviscid flow: Euler equations of Motion
For an ideal gas the equation of state
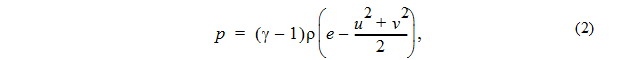
(p the pressure,rho the density, e the total energy und gamma the ratio of specific heats of the gas).
These Euler equations include the modelling of rotational flow.
Potential theory:
Potential flow simplification: Irrotationality, isoenergetic flow
Potential Phi, with grad(Phi) = (u, v); Streamfunction Psi
Hodograph transformation to velocity components (Q, theta) as independent variables:
Physical plane (x, y), Hodograph plane (Q, theta)
Use of dimensionless variables: velocity Q, flow angle theta, density D, local Mach number M
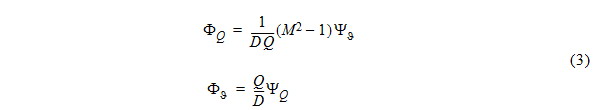
Isoenergetic relations between density, D, Mach number M and velocity Q:
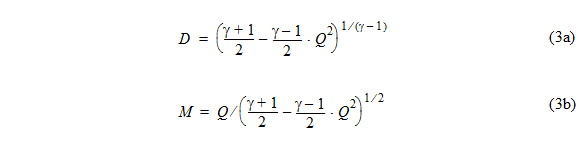
resulting in Eq. (3) to be linear because D = D(Q) and M = M(Q).
A solution Phi, Psi (Q, theta) of Eq. 3 allows for integration of the physical plane coordinates (x, y):
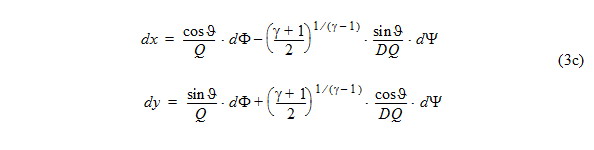
which allows to obtain flow models in the physical plane from finding solutions of Eq. (3) in the Hodograph plane
Reshaping the Hodograph variables yields a canonical form (Beltrami equations), which is the basis for inverse methods of elliptic continuation for the subsonic part, and hyperbolic mathods of characteristics for the supersonic part of transonic flow
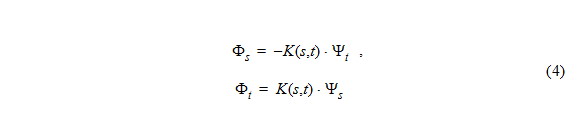
There is an analogy to electrostatic potential distributions solved by an equivalent Beltrami system, representing a 2D Ohm's law with electric potential, current strength and conductivity in a 2D conductor
Compilation of gasdynamic variables suitable for modifications of the basic equations to become design tools:
| Ratio of specific heats | 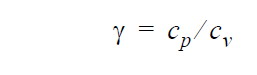 |
| Ideal gas equation of state | 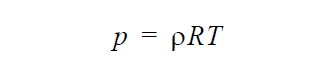 |
| Isentropic conditions | 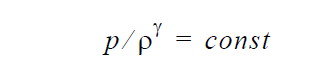 |
| Energy equation | 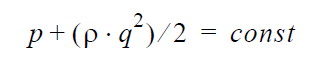 |
| Speed of sound a | 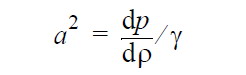 |
| Mach number | 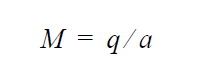 |
| Critical conditions if M = 1 | 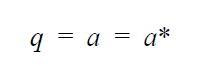 |
Parameters, made dimensionless by critical values:
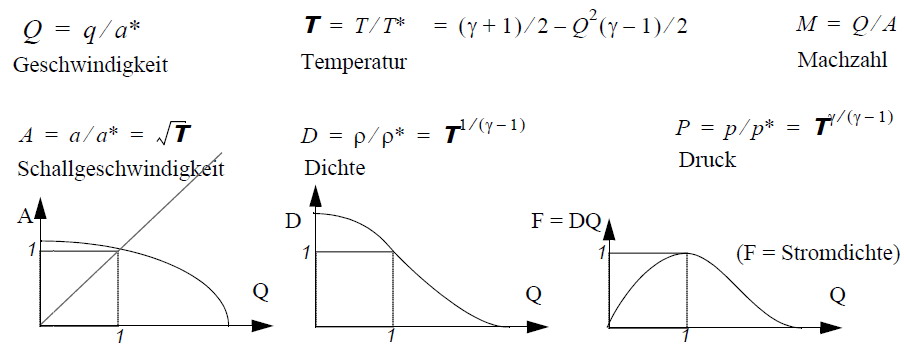
"Fictitious Gas"
Parameter manipulation to change the speed of sound to become larger than the flow speed also for conditions q > a* (= Q > 1), resulting in subsonic flow phenomena in the supercritical domain:
With unchanged definition of the speed of sound
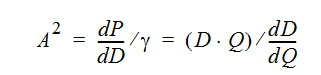
the following relations are postulated to hold within the domain Q > 1, describing the properties of a fictitious gas (F. G.) ,
with a free parameter 0 <= lambda <= 1:
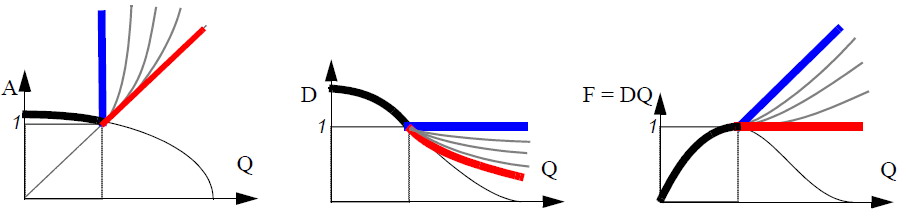
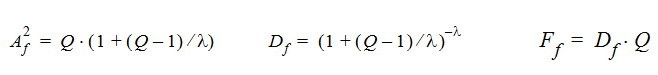
within the limits of an incompressible F. G. (D = 1), and a sonic flow F. G. (A = Q)
All cases suppress the phenomena of supersonic flow.
Interpretation of the F. G. as controlled energy addition and subtraction