3-3. Generalized small perturbation equations
Models for local and asymptotic flow phenomena:
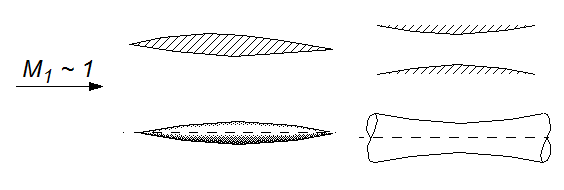
Slender bodies, thin wings, channel and nozzle flows, farfield flow structure.
With 3 switch parameters (j, k, l) the basic equations in a restriction to small perturbations of a given uniform flow may be written in a unified structure, either for the potential flow formulation:
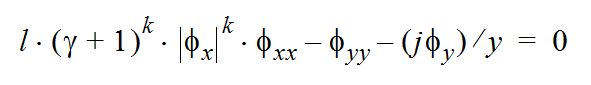 (1)
(1)
or in hodograph variables, where potential and stream function are identical with the coordinates X and Y of the physical plane and the velocity components are represented by variables U and V. These 4 variables are to be found in a 2D working plane which is a mapped hodograph plane.
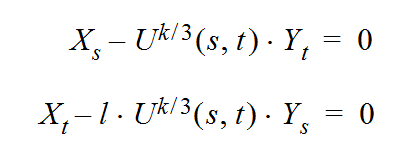
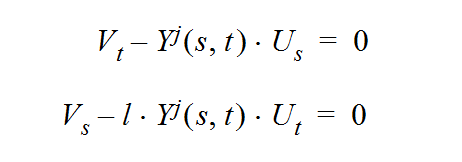 (2)
(2)
These model equations describe plane (j = 0) or axisymmetric (j = 1) flows,
linear subsonic (k=0, l=-1) or supersonic (k=0, l=1) flows,
plane transonic, (j = 0, k=1, l = -1 or 1)) flows, or
axisymmetric transonic, (j = 1, k=1, l = -1 or 1)) flows.
Note that in direct potential formulation,(1), transonic flows (k = 1) are modeled by a strongly non-linear equation for both plane or axisymmetric flows, while the hodograph equations are linear for plane flows (j = 0, k = 1) and only weakly nonlinear for axisymmetric transonic flows (j = 1, k = 1).
The variables U, V, X, Y are similarity variables and yield real physical variables (x, y) for the flow plane, and (u, v) for the velocity components by the following relations:
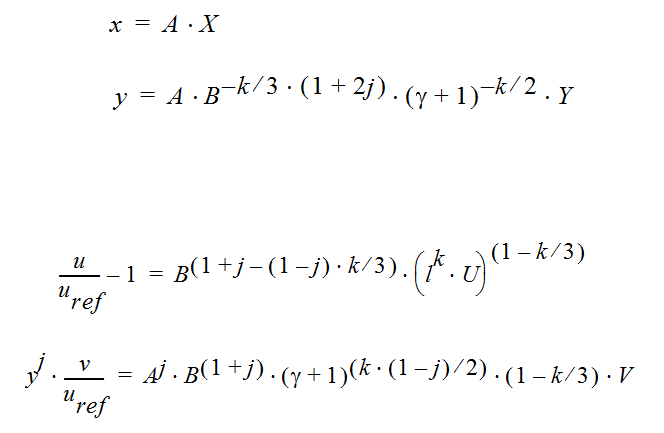 (3)
(3)
with free scaling parameters A and B. The value u(ref) represents a free-stream velocity, in case of transonic flow the critical speed of sound.